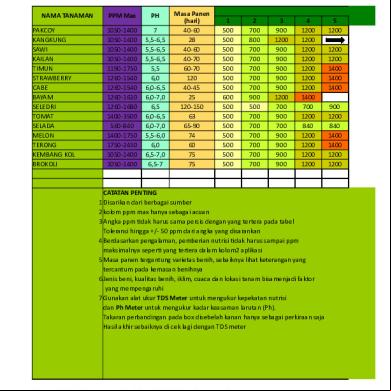
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report l4457
Overview 6h3y3j
& View Stability & Determinacy Of Trusses as PDF for free.
More details h6z72
- Words: 1,089
- Pages: 5
CE 331, Spring 2011
Stability & Determinacy of Trusses
1 / 5
The first step in analyzing a truss is to determine if the truss is stable or unstable. The truss in Figure 1a below is not stable, and is therefore not a structure. The ts of an unstable structure can be displaced without causing any of the to deform (lengthen or shorten in this case), as shown in Figure 1b.
tension
Figure 2a. Stable & Determinate Truss
compression
Figure 1a. Unstable Truss Figure 1b. In Figure 2a, a diagonal member has been added to the truss of Figure 1. This truss is stable: a the horizontal load shown in Figure 2b causes the diagonal to stretch and the shown in blue to shorten. The ts cannot be displaced without causing to deform and therefore to resist the attempted displacement. The bar forces in the truss of Figure 2b can easily be calculated using the equations of static equilibrium and the truss is said to be statically determinate. compression
Figure 2b.
In Figure 3 below we have added another member to the truss of Figure 2. The bar forces of this truss cannot be calculated using the equilibrium equations alone and the truss is said to be statically indeterminate. The forces can be calculated by hand for the truss in Figure 3, but it is an involved procedure. Most practicing structural engineers would calculate the bar forces using a structural analysis computer program.
diagonals are not connected
Figure 3. Indeterminate Truss
CE 331, Spring 2011
Stability & Determinacy of Trusses
2 / 5
Statically indeterminate trusses differ from statically determinate trusses in several ways besides complexity of analysis by hand calculations. • Indeterminate trusses are redundant. As illustrated by the trusses in Figures 1 through 3, the indeterminate truss of Figure 3 has one additional member than is required for stability. If one of the diagonals in Figure 3 fails, for example, the load will be shifted to the other diagonal and the truss will not collapse. If the single diagonal of Figure 2 fails, however, the truss will collapse. •
Indeterminate trusses can be more structurally efficient (where structural efficiency = load at failure / weight of structure). The two trusses shown in Figure 4 below have identical and loads (a total of 80 kips each), yet the forces in the chords (the horizontal ) are very different. As seen in the figure, the maximum chord force in the indeterminate continuous‐span truss is 21.4kips and the maximum force in the two simple span trusses are 26.7k.
Figure 4a. Chord forces (in kips) in a truss with two continuous spans (indeterminate)
Figure 4b. Chord forces (in kips) in two simple span trusses (determinate)
CE 331, Spring 2011
•
Stability & Determinacy of Trusses
3 / 5
Indeterminate trusses are much more effected by settlement. settlement can cause large forces in indeterminate trusses, as illustrated in Figure 5 below. Indeterminate trusses are not affected by settlement, as seen in Figure 6.
(a)
(b) Figure 5. Deflected shape (a) and chord forces (b) in kips of two‐span continuous truss due to 1” settlement of center .
(a)
(b) Figure 6. Deflected shape (a) and chord forces (b) in kips of two simple‐span trusses due to 1” settlement of center .
Stability & Determinacy of Trusses
CE 331, Spring 2011
4 / 5
Procedures are presented below for determining if a structure is stable or unstable, and determinate or indeterminate. The first procedure involves counting the number of unknown forces, counting the number of equilibrium equations, and comparing the two numbers. This procedure is fairly straightforward to follow but is not foolproof, since it does not for the arrangement of and s. The second procedure is harder to implement, but serves as a good check on the results from the first procedure. Counting Procedure. The procedure is derived using the simple truss below left. The truss is “exploded” into nine separate free‐body diagrams, one for each member and one for each t.
Number of Unknowns = 13 forces
•
2 forces per member x 5 = 10 (the forces are the ts are equal and opposite to the adjacent member‐end force and are not counted)
•
3 reactions
Number of Equations = 13 • •
1 equation per member x 5 = 5 (Σ FII) 2 equations per t x 4 ts = 8 (Σ FH, Σ FV)
Shortcut: (Used by some books) Number of Unknowns = 13 8 • •
2 1 forces per member x 5 = 10 5 3 reactions
Number of Equations = 13 8 • •
1 equation per member x 5 = 5 2 equations per t x 4 ts = 8
Since the number of unknown forces = the number of equations, the structure is statically determinate (the member forces can be calculated using equilibrium equations).
Stability & Determinacy of Trusses
CE 331, Spring 2011
5 / 5
In general: If
The structure is
number of unknowns
< number of equations
Unstable
number of unknowns
= number of equations
Stable & Determinate
number of unknowns > number of equations Indeterminate The procedure outlined above does not always work with regard to stability. For example, the truss below has the same number of unknowns as equations, yet it is unstable as illustrated in the second figure below. Number of Unknowns = 9 member forces + 3 reactions = 12 Number of Equations = 6 ts x 2 eqns/t = 12 The structure displaces without any deforming. No member deformation means no resistance to structure displacement. The structure is therefore unstable. The figure above suggests an alternate procedure (the displaced shape procedure) of determining whether a structure is stable or unstable. • If the displaced shape of the structure can be drawn so that no deform, the structure is unstable. •
If the displaced shape cannot be drawn without causing a member to deform, the structure is stable.
The method can be extended to also determine if a structure is statically indeterminate. • If removal of one constraint (a or a member force) causes the structure to be unstable (i.e. the structure can be displaced without deforming a member), then the original structure is stable and determinate (see Figure 2 for an example). •
If two or more constraints need to be removed to cause the structure to be unstable, the original structure is stable and indeterminate (see Figure 3 for an example).
Stability & Determinacy of Trusses
1 / 5
The first step in analyzing a truss is to determine if the truss is stable or unstable. The truss in Figure 1a below is not stable, and is therefore not a structure. The ts of an unstable structure can be displaced without causing any of the to deform (lengthen or shorten in this case), as shown in Figure 1b.
tension
Figure 2a. Stable & Determinate Truss
compression
Figure 1a. Unstable Truss Figure 1b. In Figure 2a, a diagonal member has been added to the truss of Figure 1. This truss is stable: a the horizontal load shown in Figure 2b causes the diagonal to stretch and the shown in blue to shorten. The ts cannot be displaced without causing to deform and therefore to resist the attempted displacement. The bar forces in the truss of Figure 2b can easily be calculated using the equations of static equilibrium and the truss is said to be statically determinate. compression
Figure 2b.
In Figure 3 below we have added another member to the truss of Figure 2. The bar forces of this truss cannot be calculated using the equilibrium equations alone and the truss is said to be statically indeterminate. The forces can be calculated by hand for the truss in Figure 3, but it is an involved procedure. Most practicing structural engineers would calculate the bar forces using a structural analysis computer program.
diagonals are not connected
Figure 3. Indeterminate Truss
CE 331, Spring 2011
Stability & Determinacy of Trusses
2 / 5
Statically indeterminate trusses differ from statically determinate trusses in several ways besides complexity of analysis by hand calculations. • Indeterminate trusses are redundant. As illustrated by the trusses in Figures 1 through 3, the indeterminate truss of Figure 3 has one additional member than is required for stability. If one of the diagonals in Figure 3 fails, for example, the load will be shifted to the other diagonal and the truss will not collapse. If the single diagonal of Figure 2 fails, however, the truss will collapse. •
Indeterminate trusses can be more structurally efficient (where structural efficiency = load at failure / weight of structure). The two trusses shown in Figure 4 below have identical and loads (a total of 80 kips each), yet the forces in the chords (the horizontal ) are very different. As seen in the figure, the maximum chord force in the indeterminate continuous‐span truss is 21.4kips and the maximum force in the two simple span trusses are 26.7k.
Figure 4a. Chord forces (in kips) in a truss with two continuous spans (indeterminate)
Figure 4b. Chord forces (in kips) in two simple span trusses (determinate)
CE 331, Spring 2011
•
Stability & Determinacy of Trusses
3 / 5
Indeterminate trusses are much more effected by settlement. settlement can cause large forces in indeterminate trusses, as illustrated in Figure 5 below. Indeterminate trusses are not affected by settlement, as seen in Figure 6.
(a)
(b) Figure 5. Deflected shape (a) and chord forces (b) in kips of two‐span continuous truss due to 1” settlement of center .
(a)
(b) Figure 6. Deflected shape (a) and chord forces (b) in kips of two simple‐span trusses due to 1” settlement of center .
Stability & Determinacy of Trusses
CE 331, Spring 2011
4 / 5
Procedures are presented below for determining if a structure is stable or unstable, and determinate or indeterminate. The first procedure involves counting the number of unknown forces, counting the number of equilibrium equations, and comparing the two numbers. This procedure is fairly straightforward to follow but is not foolproof, since it does not for the arrangement of and s. The second procedure is harder to implement, but serves as a good check on the results from the first procedure. Counting Procedure. The procedure is derived using the simple truss below left. The truss is “exploded” into nine separate free‐body diagrams, one for each member and one for each t.
Number of Unknowns = 13 forces
•
2 forces per member x 5 = 10 (the forces are the ts are equal and opposite to the adjacent member‐end force and are not counted)
•
3 reactions
Number of Equations = 13 • •
1 equation per member x 5 = 5 (Σ FII) 2 equations per t x 4 ts = 8 (Σ FH, Σ FV)
Shortcut: (Used by some books) Number of Unknowns = 13 8 • •
2 1 forces per member x 5 = 10 5 3 reactions
Number of Equations = 13 8 • •
1 equation per member x 5 = 5 2 equations per t x 4 ts = 8
Since the number of unknown forces = the number of equations, the structure is statically determinate (the member forces can be calculated using equilibrium equations).
Stability & Determinacy of Trusses
CE 331, Spring 2011
5 / 5
In general: If
The structure is
number of unknowns
< number of equations
Unstable
number of unknowns
= number of equations
Stable & Determinate
number of unknowns > number of equations Indeterminate The procedure outlined above does not always work with regard to stability. For example, the truss below has the same number of unknowns as equations, yet it is unstable as illustrated in the second figure below. Number of Unknowns = 9 member forces + 3 reactions = 12 Number of Equations = 6 ts x 2 eqns/t = 12 The structure displaces without any deforming. No member deformation means no resistance to structure displacement. The structure is therefore unstable. The figure above suggests an alternate procedure (the displaced shape procedure) of determining whether a structure is stable or unstable. • If the displaced shape of the structure can be drawn so that no deform, the structure is unstable. •
If the displaced shape cannot be drawn without causing a member to deform, the structure is stable.
The method can be extended to also determine if a structure is statically indeterminate. • If removal of one constraint (a or a member force) causes the structure to be unstable (i.e. the structure can be displaced without deforming a member), then the original structure is stable and determinate (see Figure 2 for an example). •
If two or more constraints need to be removed to cause the structure to be unstable, the original structure is stable and indeterminate (see Figure 3 for an example).