Rumus Luas Permukaan Limas 1ju2k
This document was ed by and they confirmed that they have the permission to share it. If you are author or own the copyright of this book, please report to us by using this report form. Report l4457
Overview 6h3y3j
& View Rumus Luas Permukaan Limas as PDF for free.
More details h6z72
- Words: 1,578
- Pages: 21
Rumus luas permukaan limas Asal-uslu rumus luas permukaan limas Sama halnya dengan prisma, luas permukaan limas pun dapat diperoleh dengan cara menentukan jaring-jaring limas tersebut. Kemudian, menjumlahkan luas bangun datar dari jaring-jaring yang terbentuk. Untuk lebih jelasnya, coba pelajari gambar dan uraian berikut ini!
Gambar: Asal Usul Rumus Luas Permukaan Limas
Gambar di atas memperlihatkan sebuah limas segiempat E.ABCD beserta jaring-jaringnya. Dengan demikian, luas permukaan limas tersebut adalah sebagai berikut. Luas permukaan limas E. ABCD = luas ABCD + luas ΔABE + luas ΔBCE + luas ΔCDE + luas ΔADE = luas ABCD + (luas ΔABE + luas ΔBCE + luas ΔCDE + luas ΔADE) Secara umum, luas permukaan limas adalah sebagai berikut.
Luas permukaan limas = luas alas + jumlah luas sisi-sisi tegak
Rumus Volume Limas Asal-usul rumus volume limas Perhatikan gambar kubus di bawah ini dengan seksama!
Gambar tersebut diataas menunjukkan sebuah kubus ABCD.EFGH. Kubus tersebut memiliki 4 buah diagonal ruang yang saling berpotongan di titik O. Jika diamati secara cermat, keempat diagonal ruang tersebut membentuk 6 buah limas segiempat, yaitu limas segiempat O.ABCD, O.EFGH, O.ABFE, O.BCGF, O.CDHG,
dan O.DAEH. Dengan demikian, volume kubus ABCD.EFGH merupakan gabungan volume keenam limas tersebut. 6 × volume limas O.ABCD = volume kubus ABCD.EFGH
Jadi, rumus volume limas dapat dinyatakan sebagai berikut.
Volume limas = ⅓ × luas alas × tinggi
Rumus luas permukaan kerucut Asal-usul rumus luas permukaan kerucut Perhatikan jaring-jaring kerucut berikut ini, yang merupakan hasil dari bangun kerucut yang dibelah!
Gambar: jaring-jaring kerucut
Berdasarkan gambar jaring-jaring kerucut di atas, maka gambar tersebut terdiri atas; • juring lingkaran CDD' yang merupakan selimut kerucut. • lingkaran dengan jari-jari r yang merupakan sisi alas kerucut.
Pada Gambar tersebut di atas, terlihat bahwa panjang jarijari juring lingkaran sama dengan s (garis pelukis kerucut). Adapun panjang busur DD' sama dengan keliling alas kerucut, yaitu 2πr. Jadi, luas selimut kerucut sama dengan luas juring CDD'.
Jadi, luas selimut kerucut = πrs. Luas permukaan kerucut = luas selimut + luas alas = πrs + πr2 = πr (s + r) Dengan demikian, pada kerucut berlaku rumus sebagai berikut.
Luas selimut kerucut = πrs Luas permukaan kerucut = πr (s + r)
Rumus volume kerucut Asal-usul rumus volume kerucut Perhatikan dan bandingkan gambar di bawah ini dengan cermat!
Dapatkah kalian menemukan persamaan antara gambar (a) dan gambar (b)? Pada dasarnya, kerucut merupakan limas karena memiliki titik puncak sehingga volume kerucut sama dengan volume limas, yaitu 1/3 kali luas alas kali tinggi. Oleh karena alas kerucut berbentuk lingkaran, volume kerucut dinyatakan oleh rumus sebagai berikut.
Volume kerucut = 1/3 x luas alas x tinggi = 1/3 x πr2t
Rumus luas permukaan bola Asal-usul rumus permukaan bola Untuk mendapatkan rumus luas permukaan bola, tidak ada salahnya kita melakukan kegiatan berikut ini untuk menguji rumus luas permukaan bola! Perhatikan pula gambargambar berikut ini! 1. Sediakan sebuah bola berukuran sedang, misalnya bola sepak, benang kasur, karton, penggaris, dan pulpen. 2. Ukurlah keliling bola tersebut menggunakan benang kasur. 3. Lilitkan benang kasur pada permukaan setengah bola sampai penuh, seperti pada gambar (i).
4. Buatlah persegipanjang dari kertas karton dengan ukuran panjang sama dengan keliling bola dan lebar sama dengan diameter bola seperti pada gambar (ii). 5. Lilitkan benang yang tadi digunakan untuk melilit permukaan setengah bola pada persegipanjang yang kamu buat tadi. Lilitkan sampai habis.
Gambar: ii
6. Jika kamu melakukannya dengan benar, tampak bahwa benang dapat menutupi persegi panjang selebar jari-jari bola (r).
7. Hitunglah luas persegi panjang yang telah ditutupi benang. Dapatkah kamu menemukan hubungannya dengan luas permukaan setengah bola? Dari kegiatan di atas, jelaslah bahwa luas permukaan setengah bola sama dengan luas persegipanjang. Luas permukaan setengah bola = luas persegi panjang =p×l = 2πr× r = 2π r2 Sehingga, luas permukaan bola = 2 × luas permukaan setengah bola = 2 × 2πr2 = 4πr2
Jadi, luas permukaan bola dinyatakan dengan rumus sebagai berikut.
Luas permukaan bola = 4πr2
Rumus Volume Bola Asal-usul rumus volume bola Untuk mengetahui rumus volume bola, dapat dilakukan salah satunya dengan melakukan kegiatan berikut ini. 1. Siapkan sebuah wadah yang berbentuk setengah bola berjari-jari r (wadah (i)) dan sebuah wadah yang berbentuk kerucut berjari-jari r dan tingginya 2r (wadah (ii)).
2. Isikan pasir ke wadah (ii) sampai penuh. 3. Pindahkan pasir di dalam wadah (ii) ke wadah (i). Apakah yang terjadi? Dari kegiatan di atas, dapat dilihat bahwa volume pasir yang dituangkan ke dalam wadah setengah bola tidak berubah. Ini berarti, untuk bangun setengah bola, dan kerucut yang berjari-jari sama, dan tinggi kerucut sama dengan dua kali jari-jarinya maka: Volume setengah bola = volume kerucut 1/2 volume bola = 1/3 πr2t volume bola = 2/3πr2(2r) = 4/3πr3
Jadi, volume bola dinyatakan dengan rumus sebagai berikut.
Volume bola = 4/3πr 3
Rumus luas permukaan tabung Asal-usul rumus luas permukaan tabung Perhatikan kembali Gambar tabung berikut ini .
Jika tabung pada gambar tersebut dipotong sepanjang garis AD, keliling sisi alas, dan keliling sisi atasnya, akan diperoleh jaring-jaring tabung seperti pada gambar di bawah ini.
Gambar: Jaring-jaring Tabung
Selimut tabung pada Gambar tersebut di atas berbentuk persegipanjang dengan panjang AA' =DD' = keliling alas tabung = 2πr dan lebar AD =A' D' = tinggi tabung = t. Jadi, luas selimut tabung = luas persegipanjang = p × l = 2πrt. Luas permukaan tabung merupakan gabungan luas selimut tabung, luas sisi alas, dan luas sisi atas tabung.
Luas permukaan tabung = luas selimut + luas sisi alas + luas sisi atas = 2πrt + πr2 +πr2 = 2πrt + 2πr2 = 2πr (r + t) Dengan demikian, untuk tabung yang tertutup, berlaku rumus sebagai berikut.
Luas permukaan tabung = 2πr (r + t)
Rumus Volume tabung Asal-usul rumus volume tabung Pada dasarnya, tabung juga merupakan prisma karena bidang alas dan bidang atas tabung sejajar dan kongruen. Untuk lebih jelasnya, perhatikan Gambar berikut ini.
Dengan demikian, volume tabung sama dengan volume prisma, yaitu luas alas dikali tinggi. Oleh karena alas tabung berbentuk lingkaran, volume tabung dinyatakan sebagai berikut. Volume tabung = luas alas × tinggi = πr2t
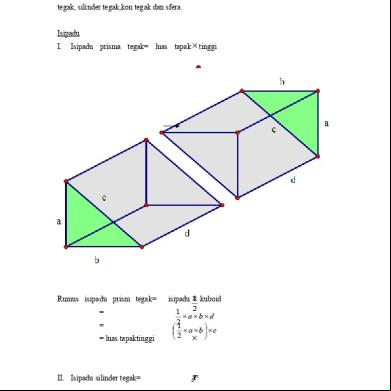
Rumus luas permukaan prisma Sama seperti kubus dan balok, asal usul menentukan luas permukaan prisma dapat dihitung menggunakan jaringjaring prisma tersebut. Caranya adalah dengan menjumlahkan semua luas bangun datar pada jaring-jaring prisma.
Untuk lebih jelasnya silahkan perhatikan prisma segitiga berikut ini beserta jaring-jaringnya!
Gambar: Asal Usul Rumus Luas permukaan prisma
Dari gambar tersebut di atas, terlihat bahwa prisma segitiga ABC.DEF memiliki sepasang segitiga yang identik dan tiga buah persegipanjang sebagai sisi tegak. Dengan demikian, luas permukaan prisma segitiga tersebut adalah; Luas permukaan prisma = luas ΔABC + luas ΔDEF + luas EDAB + luas DFCA + luas FEBC = 2 x luas ΔABC + luas EDBA + luas DFAC + luas FEBC = (2 x luas alas) + (luas bidangbidang tegak) Jadi, luas permukaan dapat dinyatakan dengan rumus sebagai berikut.
Luas permukaan prisma = 2 x luas alas + luas bidang-bidang tegak
Rumus volume prisma Untuk lebih memahami asal-usul rumus volume prisma, silahkan perhatikan gambar berikut ini!
Gambar: Asal usul rumus volume prisma
Pada gambar tersebut di atas, memperlihatkan sebuah balok ABCD.EFGH yang dibagi dua secara melintang. Ternyata, hasil belahan balok tersebut membentuk prisma segitiga, seperti pada Gambar (b). Perhatikan prisma segitiga BCD.FGH pada Gambar (c) . Dengan demikian, volume prisma segitiga adalah setengah kali volume balok. Volume prisma BCD.FGH = ½ × volume balok ABCD.EFGH = ½ × (p × l × t) = ( ½ × p × l) × t = luas alas × tinggi Jadi, volume prisma dapat dinyatakan dengan rumus sebagai berikut.
Volume prisma = luas alas × tinggi
Proyeksi Titik ke Garis Untuk proyeksi titik ke garis, titik sebagai proyeksian dan garis sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi titik P ke segmen garis AB yang hasil proyeksinya adalah titik R yang ada pada garis AB. Titik R tersebut dikatakan hasil proyeksi jika garis PR (putus-putus) tegak lurus dengan garis AB. Proyeksi Titik ke Bidang Untuk proyeksi titik ke bidang, titik sebagai proyeksian dan bidang sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi titik P ke bidang W yang hasil proyeksinya adalah titik R yang ada pada bidang W. Titik R tersebut dikatakan hasil proyeksi jika garis PR (putus-putus) tegak lurus dengan bidang W. Proyeksian = titik P, hasil proyeksian = titik R, dan proyeksitor = bidang W. Proyeksi garis ke Garis Untuk proyeksi garis ke garis, garis pertama sebagai proyeksian dan garis keuad sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi segmen garis AB ke garis g yang hasil proyeksinya adalah segmen garis PR yang ada pada garis g. Segmen garis PR tersebut dikatakan hasil proyeksi jika garis putus-
putus tegak lurus dengan garis g. Proyeksian = segmen garis AB, hasil proyeksian = segmen garis PR, dan proyeksitor = garis g. Proyeksi Garis ke Bidang Untuk proyeksi garis ke bidang, garis sebagai proyeksian dan bidang sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi segmen garis AB ke bidang W yang hasil proyeksinya adalah segmen garis PR yang ada pada bidang W. Segmen garis PR tersebut dikatakan hasil proyeksi jika garis putus-putus tegak lurus dengan bidang W. Proyeksian = segmen garis AB, hasil proyeksian = segmen garis PR, dan proyeksitor = bidang W.
Proyeksi Bidang ke Bidang Untuk proyeksi bidang ke bidang, bidang pertama sebagai proyeksian dan bidang kedua sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi bidang V ke bidang W yang hasil proyeksinya adalah bidang Y. Bidang Y tersebut dikatakan hasil proyeksi jika garis putusputus warna merah tegak lurus dengan bidang W. Proyeksian = bidang V, hasil proyeksian = bidang Y, dan proyeksitor = bidang W.
Gambar: Asal Usul Rumus Luas Permukaan Limas
Gambar di atas memperlihatkan sebuah limas segiempat E.ABCD beserta jaring-jaringnya. Dengan demikian, luas permukaan limas tersebut adalah sebagai berikut. Luas permukaan limas E. ABCD = luas ABCD + luas ΔABE + luas ΔBCE + luas ΔCDE + luas ΔADE = luas ABCD + (luas ΔABE + luas ΔBCE + luas ΔCDE + luas ΔADE) Secara umum, luas permukaan limas adalah sebagai berikut.
Luas permukaan limas = luas alas + jumlah luas sisi-sisi tegak
Rumus Volume Limas Asal-usul rumus volume limas Perhatikan gambar kubus di bawah ini dengan seksama!
Gambar tersebut diataas menunjukkan sebuah kubus ABCD.EFGH. Kubus tersebut memiliki 4 buah diagonal ruang yang saling berpotongan di titik O. Jika diamati secara cermat, keempat diagonal ruang tersebut membentuk 6 buah limas segiempat, yaitu limas segiempat O.ABCD, O.EFGH, O.ABFE, O.BCGF, O.CDHG,
dan O.DAEH. Dengan demikian, volume kubus ABCD.EFGH merupakan gabungan volume keenam limas tersebut. 6 × volume limas O.ABCD = volume kubus ABCD.EFGH
Jadi, rumus volume limas dapat dinyatakan sebagai berikut.
Volume limas = ⅓ × luas alas × tinggi
Rumus luas permukaan kerucut Asal-usul rumus luas permukaan kerucut Perhatikan jaring-jaring kerucut berikut ini, yang merupakan hasil dari bangun kerucut yang dibelah!
Gambar: jaring-jaring kerucut
Berdasarkan gambar jaring-jaring kerucut di atas, maka gambar tersebut terdiri atas; • juring lingkaran CDD' yang merupakan selimut kerucut. • lingkaran dengan jari-jari r yang merupakan sisi alas kerucut.
Pada Gambar tersebut di atas, terlihat bahwa panjang jarijari juring lingkaran sama dengan s (garis pelukis kerucut). Adapun panjang busur DD' sama dengan keliling alas kerucut, yaitu 2πr. Jadi, luas selimut kerucut sama dengan luas juring CDD'.
Jadi, luas selimut kerucut = πrs. Luas permukaan kerucut = luas selimut + luas alas = πrs + πr2 = πr (s + r) Dengan demikian, pada kerucut berlaku rumus sebagai berikut.
Luas selimut kerucut = πrs Luas permukaan kerucut = πr (s + r)
Rumus volume kerucut Asal-usul rumus volume kerucut Perhatikan dan bandingkan gambar di bawah ini dengan cermat!
Dapatkah kalian menemukan persamaan antara gambar (a) dan gambar (b)? Pada dasarnya, kerucut merupakan limas karena memiliki titik puncak sehingga volume kerucut sama dengan volume limas, yaitu 1/3 kali luas alas kali tinggi. Oleh karena alas kerucut berbentuk lingkaran, volume kerucut dinyatakan oleh rumus sebagai berikut.
Volume kerucut = 1/3 x luas alas x tinggi = 1/3 x πr2t
Rumus luas permukaan bola Asal-usul rumus permukaan bola Untuk mendapatkan rumus luas permukaan bola, tidak ada salahnya kita melakukan kegiatan berikut ini untuk menguji rumus luas permukaan bola! Perhatikan pula gambargambar berikut ini! 1. Sediakan sebuah bola berukuran sedang, misalnya bola sepak, benang kasur, karton, penggaris, dan pulpen. 2. Ukurlah keliling bola tersebut menggunakan benang kasur. 3. Lilitkan benang kasur pada permukaan setengah bola sampai penuh, seperti pada gambar (i).
4. Buatlah persegipanjang dari kertas karton dengan ukuran panjang sama dengan keliling bola dan lebar sama dengan diameter bola seperti pada gambar (ii). 5. Lilitkan benang yang tadi digunakan untuk melilit permukaan setengah bola pada persegipanjang yang kamu buat tadi. Lilitkan sampai habis.
Gambar: ii
6. Jika kamu melakukannya dengan benar, tampak bahwa benang dapat menutupi persegi panjang selebar jari-jari bola (r).
7. Hitunglah luas persegi panjang yang telah ditutupi benang. Dapatkah kamu menemukan hubungannya dengan luas permukaan setengah bola? Dari kegiatan di atas, jelaslah bahwa luas permukaan setengah bola sama dengan luas persegipanjang. Luas permukaan setengah bola = luas persegi panjang =p×l = 2πr× r = 2π r2 Sehingga, luas permukaan bola = 2 × luas permukaan setengah bola = 2 × 2πr2 = 4πr2
Jadi, luas permukaan bola dinyatakan dengan rumus sebagai berikut.
Luas permukaan bola = 4πr2
Rumus Volume Bola Asal-usul rumus volume bola Untuk mengetahui rumus volume bola, dapat dilakukan salah satunya dengan melakukan kegiatan berikut ini. 1. Siapkan sebuah wadah yang berbentuk setengah bola berjari-jari r (wadah (i)) dan sebuah wadah yang berbentuk kerucut berjari-jari r dan tingginya 2r (wadah (ii)).
2. Isikan pasir ke wadah (ii) sampai penuh. 3. Pindahkan pasir di dalam wadah (ii) ke wadah (i). Apakah yang terjadi? Dari kegiatan di atas, dapat dilihat bahwa volume pasir yang dituangkan ke dalam wadah setengah bola tidak berubah. Ini berarti, untuk bangun setengah bola, dan kerucut yang berjari-jari sama, dan tinggi kerucut sama dengan dua kali jari-jarinya maka: Volume setengah bola = volume kerucut 1/2 volume bola = 1/3 πr2t volume bola = 2/3πr2(2r) = 4/3πr3
Jadi, volume bola dinyatakan dengan rumus sebagai berikut.
Volume bola = 4/3πr 3
Rumus luas permukaan tabung Asal-usul rumus luas permukaan tabung Perhatikan kembali Gambar tabung berikut ini .
Jika tabung pada gambar tersebut dipotong sepanjang garis AD, keliling sisi alas, dan keliling sisi atasnya, akan diperoleh jaring-jaring tabung seperti pada gambar di bawah ini.
Gambar: Jaring-jaring Tabung
Selimut tabung pada Gambar tersebut di atas berbentuk persegipanjang dengan panjang AA' =DD' = keliling alas tabung = 2πr dan lebar AD =A' D' = tinggi tabung = t. Jadi, luas selimut tabung = luas persegipanjang = p × l = 2πrt. Luas permukaan tabung merupakan gabungan luas selimut tabung, luas sisi alas, dan luas sisi atas tabung.
Luas permukaan tabung = luas selimut + luas sisi alas + luas sisi atas = 2πrt + πr2 +πr2 = 2πrt + 2πr2 = 2πr (r + t) Dengan demikian, untuk tabung yang tertutup, berlaku rumus sebagai berikut.
Luas permukaan tabung = 2πr (r + t)
Rumus Volume tabung Asal-usul rumus volume tabung Pada dasarnya, tabung juga merupakan prisma karena bidang alas dan bidang atas tabung sejajar dan kongruen. Untuk lebih jelasnya, perhatikan Gambar berikut ini.
Dengan demikian, volume tabung sama dengan volume prisma, yaitu luas alas dikali tinggi. Oleh karena alas tabung berbentuk lingkaran, volume tabung dinyatakan sebagai berikut. Volume tabung = luas alas × tinggi = πr2t
Rumus luas permukaan prisma Sama seperti kubus dan balok, asal usul menentukan luas permukaan prisma dapat dihitung menggunakan jaringjaring prisma tersebut. Caranya adalah dengan menjumlahkan semua luas bangun datar pada jaring-jaring prisma.
Untuk lebih jelasnya silahkan perhatikan prisma segitiga berikut ini beserta jaring-jaringnya!
Gambar: Asal Usul Rumus Luas permukaan prisma
Dari gambar tersebut di atas, terlihat bahwa prisma segitiga ABC.DEF memiliki sepasang segitiga yang identik dan tiga buah persegipanjang sebagai sisi tegak. Dengan demikian, luas permukaan prisma segitiga tersebut adalah; Luas permukaan prisma = luas ΔABC + luas ΔDEF + luas EDAB + luas DFCA + luas FEBC = 2 x luas ΔABC + luas EDBA + luas DFAC + luas FEBC = (2 x luas alas) + (luas bidangbidang tegak) Jadi, luas permukaan dapat dinyatakan dengan rumus sebagai berikut.
Luas permukaan prisma = 2 x luas alas + luas bidang-bidang tegak
Rumus volume prisma Untuk lebih memahami asal-usul rumus volume prisma, silahkan perhatikan gambar berikut ini!
Gambar: Asal usul rumus volume prisma
Pada gambar tersebut di atas, memperlihatkan sebuah balok ABCD.EFGH yang dibagi dua secara melintang. Ternyata, hasil belahan balok tersebut membentuk prisma segitiga, seperti pada Gambar (b). Perhatikan prisma segitiga BCD.FGH pada Gambar (c) . Dengan demikian, volume prisma segitiga adalah setengah kali volume balok. Volume prisma BCD.FGH = ½ × volume balok ABCD.EFGH = ½ × (p × l × t) = ( ½ × p × l) × t = luas alas × tinggi Jadi, volume prisma dapat dinyatakan dengan rumus sebagai berikut.
Volume prisma = luas alas × tinggi
Proyeksi Titik ke Garis Untuk proyeksi titik ke garis, titik sebagai proyeksian dan garis sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi titik P ke segmen garis AB yang hasil proyeksinya adalah titik R yang ada pada garis AB. Titik R tersebut dikatakan hasil proyeksi jika garis PR (putus-putus) tegak lurus dengan garis AB. Proyeksi Titik ke Bidang Untuk proyeksi titik ke bidang, titik sebagai proyeksian dan bidang sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi titik P ke bidang W yang hasil proyeksinya adalah titik R yang ada pada bidang W. Titik R tersebut dikatakan hasil proyeksi jika garis PR (putus-putus) tegak lurus dengan bidang W. Proyeksian = titik P, hasil proyeksian = titik R, dan proyeksitor = bidang W. Proyeksi garis ke Garis Untuk proyeksi garis ke garis, garis pertama sebagai proyeksian dan garis keuad sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi segmen garis AB ke garis g yang hasil proyeksinya adalah segmen garis PR yang ada pada garis g. Segmen garis PR tersebut dikatakan hasil proyeksi jika garis putus-
putus tegak lurus dengan garis g. Proyeksian = segmen garis AB, hasil proyeksian = segmen garis PR, dan proyeksitor = garis g. Proyeksi Garis ke Bidang Untuk proyeksi garis ke bidang, garis sebagai proyeksian dan bidang sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi segmen garis AB ke bidang W yang hasil proyeksinya adalah segmen garis PR yang ada pada bidang W. Segmen garis PR tersebut dikatakan hasil proyeksi jika garis putus-putus tegak lurus dengan bidang W. Proyeksian = segmen garis AB, hasil proyeksian = segmen garis PR, dan proyeksitor = bidang W.
Proyeksi Bidang ke Bidang Untuk proyeksi bidang ke bidang, bidang pertama sebagai proyeksian dan bidang kedua sebagai proyeksitor. Berikut gambar proyeksinya :
Dari gambar, proyeksi bidang V ke bidang W yang hasil proyeksinya adalah bidang Y. Bidang Y tersebut dikatakan hasil proyeksi jika garis putusputus warna merah tegak lurus dengan bidang W. Proyeksian = bidang V, hasil proyeksian = bidang Y, dan proyeksitor = bidang W.